Пет правилних полиедара |
|||||
|---|---|---|---|---|---|
| Име | Тетраедар | Хексаедар или Коцка |
Октаедар | Додекаедар | Икосаедар |
| Слика | (Анимација) |
(Анимација) |
(Анимација) |
(Анимација) |
(Анимација) |
| Размотана фигура |
|||||
| Површи | 4 троугла | 6 квадрата | 8 троуглова | 12 петоуглова | 20 троуглова |
| Број ивица/темена | 6 / 4 | 12 / 8 | 12 / 6 | 30 / 20 | 30 / 12 |
| Број ивица у једном темену |
3 | 3 | 4 | 3 | 5 |
четвртак, 5. септембар 2024.
PRAVILNI POLIEDRI
PRIZMA
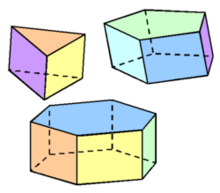 Prizma je geometrijsko telo ograničeno sa dva
paralelna i podudarna mnogougla i onoliko paralelograma koliko stranica
ima jedan od tih mnogouglova. Mnogouglove nazivamo osnovama prizme, a
paralelogrami su bočne strane prizme.
Prizma je geometrijsko telo ograničeno sa dva
paralelna i podudarna mnogougla i onoliko paralelograma koliko stranica
ima jedan od tih mnogouglova. Mnogouglove nazivamo osnovama prizme, a
paralelogrami su bočne strane prizme.
Bočne strane prizme obrazuju omotač
prizme.
Visina prizme je rastojanje između njenih osnova, tj. visina je dužia normale koja je spuštena iz bilo koje tačke jedne baze na ravan druge baze.
Ako su bočne ivice prizme normalne na osnovu prizme, tada je prizma prava. Ukoliko prizma nije prava, kaže se da je kosa. Visina prave prizme se poklapa sa bocnom ivicom, a bocne strane su pravougaonici.
Kad prava prizma ima pravilan mnogougao u osnovi,
ona je pravilna. Sve bocne strane pravilne prizme su podudarni pravougaonici.
Paralelopiped
je prizma cija je osnova paralelogram. Paralelopiped ima 8 temena, 12 ivica i 6 strana. Četiri bocne strane su paralelogrami kao kod svake prizme, osnove su paralelogrami po
definiciji, prema tome sve strane su paralelogrami.
POVRŠINA PRIZME
Mreža bilo koje prizme se sastoji od dve baze i omotača pa je površina svake prizme
ZAPREMINA PRIZME
V=B.H
gde je B
Primer: pravilna trostrana prizma i pravilna šestostrana prizma
















